विषय

• कदम बढ़ाने के लिए
• 3 की विधि 1: पहला सरल कार्य
• विधि 2 का 3: किसी विशिष्ट परिणाम के लिए अपेक्षित मान की गणना करना
• 3 की विधि 3: अवधारणा को समझें
• टिप्स
• नेसेसिटीज़

अपेक्षा मूल्य एक सांख्यिकीय शब्द है, और एक अवधारणा का उपयोग यह तय करने के लिए किया जाता है कि कार्रवाई कितनी उपयोगी या हानिकारक होगी। अपेक्षित मूल्य की गणना करने के लिए, किसी विशेष स्थिति में प्रत्येक परिणाम और संबंधित संभावना, या एक विशेष परिणाम होने की संभावना की एक अच्छी समझ हासिल करना आवश्यक है। नीचे दिए गए चरण आपको उम्मीद के मूल्य की अवधारणा को समझने में मदद करने के लिए कुछ उदाहरण अभ्यास प्रदान करते हैं।

कदम बढ़ाने के लिए

3 की विधि 1: पहला सरल कार्य

1. कथन पढ़ें। इससे पहले कि आप सभी संभावित परिणामों और संभावनाओं के बारे में सोचना शुरू करें, यह महत्वपूर्ण है कि आप समस्या को समझें। उदाहरण के लिए एक पासा खेल जिसकी लागत प्रति खेल € 10 है। एक हेक्स डाई एक बार लुढ़का होता है और आपकी जीत आपके रोल नंबर पर निर्भर करती है। यदि एक 6 लुढ़का है, तो आप € 30 जीतते हैं; एक 5 € 20 कमाता है; किसी भी अन्य संख्या में कुछ भी नहीं मिलता है।
2. सभी संभावित परिणामों की सूची बनाएं। यह किसी भी स्थिति में सभी संभावित परिणामों को सूचीबद्ध करने में मदद करता है। उपरोक्त उदाहरण में, 6 संभावित परिणाम हैं। ये हैं: (१) रोल १ , (5) एक 5 रोल करें और $ 10 जीतें, (6) एक 6 रोल करें और 20 डॉलर जीतें।
   • ध्यान दें कि प्रत्येक परिणाम ऊपर वर्णित की तुलना में € 10 कम है, क्योंकि आपको परिणाम की परवाह किए बिना पहले प्रति गेम € 10 का भुगतान करना होगा।
3. प्रत्येक परिणाम की संभावना निर्धारित करें। इस मामले में, किसी भी 6 परिणामों की संभावना समान है। एक यादृच्छिक संख्या के लुढ़कने की संभावना 1 में 6. है। यह लिखना आसान बनाने के लिए, हम एक कैलकुलेटर का उपयोग करके दशमलव के रूप में अंश (1/6) लिखेंगे: 0.167। प्रत्येक परिणाम के बगल में इस संभावना को लिखें, खासकर यदि आप प्रत्येक परिणाम के लिए विभिन्न संभावनाओं के साथ एक समस्या को हल करना चाहते हैं।
   • आपका 1/6 कैलकुलेटर 0.166667 जैसा कुछ बना सकता है। हम सटीकता का त्याग किए बिना गणना करना आसान बनाने के लिए इसे 0.167 पर गोल करते हैं।
   • यदि आप बहुत सटीक परिणाम चाहते हैं, तो इसे दशमलव न बनाएं, बस 1/6 सूत्र में दर्ज करें और इसे अपने कैलकुलेटर पर गणना करें।
4. प्रत्येक परिणाम का मूल्य रिकॉर्ड करें। परिणाम की $ संभावना से गुणा करें कि परिणाम की गणना करने के लिए परिणाम होगा कि कितना धन जो परिणाम अपेक्षित मूल्य में योगदान करेगा। उदाहरण के लिए, 1 रोल करने का परिणाम है - $ 10 और 1 रोल करने की संभावना 0.167 है। 1 फेंकने का मान इसलिए (-10) * (0.167) है।
   • अब इन परिणामों की गणना करने की आवश्यकता नहीं है यदि आपके पास एक कैलकुलेटर है जो एक ही समय में कई ऑपरेशन कर सकता है। यदि आप पूरे समीकरण में प्रवेश करते हैं तो आपको अधिक सटीक परिणाम मिलेगा।
5. किसी घटना के अपेक्षित मूल्य प्राप्त करने के लिए प्रत्येक परिणाम का मूल्य जोड़ें। उपरोक्त उदाहरण के साथ जारी रखने के लिए, पासा खेल का अपेक्षित मूल्य है: (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (10) * 0.167) + (20 * 0.167), या - € 1.67। इसलिए आप इस गेम (प्रति गेम) पर हर बार $ 1.67 खोने की उम्मीद कर सकते हैं।
6. अपेक्षित मूल्य की गणना के निहितार्थ क्या हैं। उपरोक्त उदाहरण में, हमने निर्धारित किया कि अपेक्षित लाभ (हानि) - € 1.67 प्रति फेंक होगा। यह 1 गेम के लिए एक असंभव परिणाम है; आप € 10 खो सकते हैं, € 10 जीत सकते हैं या € 20 जीत सकते हैं। लेकिन लंबे समय में, अपेक्षित मूल्य एक उपयोगी, औसत संभावना है। यदि आप इस गेम को खेलते रहते हैं, तो आप औसतन लगभग 1.67 डॉलर प्रति गेम खो देंगे। अपेक्षित मूल्य के बारे में सोचने का एक और तरीका खेल में कुछ लागत (या लाभ) निर्दिष्ट करना है; यदि आप इसे इसके लायक पाते हैं तो आपको केवल इस खेल को खेलना चाहिए, हर बार इस पर $ 1.67 खर्च करने के लिए पर्याप्त आनंद लें।
   • जितनी अधिक बार एक स्थिति को दोहराया जाता है, उतना ही सटीक मूल्य वास्तविक, औसत परिणाम का प्रतिनिधित्व होता है। उदाहरण के लिए, शायद आप लगातार 5 बार गेम खेलते हैं और आप हर बार हार जाते हैं, जिसके परिणामस्वरूप औसतन $ 10 का नुकसान होता है। हालांकि, यदि आप 1000 बार गेम खेलते हैं, तो औसत परिणाम प्रति खेल के अनुमानित मूल्य - € 1.67 के करीब और करीब आएगा। इस सिद्धांत को "बड़ी संख्या का नियम" कहा जाता है।

विधि 2 का 3: किसी विशिष्ट परिणाम के लिए अपेक्षित मान की गणना करना

1. किसी विशेष पैटर्न के होने से पहले आपको जितने सिक्कों की आवश्यकता होती है, उनकी गणना करने के लिए इस पद्धति का उपयोग करें। उदाहरण के लिए, जब तक आप एक पंक्ति में दो बार सिर नहीं करते तब तक आप अपेक्षित संख्या में सिक्कों का पता लगाने के लिए विधि का उपयोग कर सकते हैं। यह समस्या अपेक्षा के मानों के बारे में एक मानक समस्या की तुलना में थोड़ी पेचीदा है, इसलिए इस लेख के उपरोक्त भाग को पहले पढ़ें यदि आप अपेक्षा के मूल्य की अवधारणा से परिचित नहीं हैं।
2. मान लीजिए हम एक मान x की तलाश कर रहे हैं। आप यह निर्धारित करने की कोशिश कर रहे हैं कि एक पंक्ति में दो सिर पाने के लिए आपको कितने सिक्के औसतन पलटने होंगे। अब हम इसका उत्तर खोजने की तुलना करते हैं। हम उस उत्तर को कहते हैं जिसे हम x के लिए देख रहे हैं। हम आवश्यक तुलनात्मक कदम कदम से बनाते हैं। वर्तमान में हमारे पास निम्नलिखित हैं:
   • x = ___
3. पहले फ्लिप एक सिक्का पैदा करता है तो क्या होता है इसके बारे में सोचो। आधे मामलों में यही होगा। यदि यह मामला है, तो आपने एक रोल ओवर "बर्बाद" किया है, जबकि एक पंक्ति में दो बार सिर रोल करने का मौका नहीं बदला है। सिक्के के टॉस के रूप में, यह उम्मीद की जाती है कि आपको एक पंक्ति में दो बार सिर लाने से पहले कई बार फेंकना होगा। दूसरे शब्दों में, आप एक x संख्या को रोल करने की अपेक्षा करेंगे, साथ ही जो आपने पहले ही खेले हैं। एक समीकरण के रूप में:
   • x = (0.5) (x + 1) + ___
   • हम खाली जगह को भरने जा रहे हैं क्योंकि हम अन्य स्थितियों के बारे में सोचते रहते हैं।
   • यदि यह आसान या आवश्यक है तो आप दशमलव के बजाय भिन्न का उपयोग कर सकते हैं।
4. जब आप अपना सिर फेंकते हैं तो क्या होता है, इसके बारे में सोचें। एक 0.5 (या 1/2) मौका है कि आप पहली बार एक कप फेंक देंगे। ऐसा लगता है कि एक पंक्ति में दो बार सिर फेंकने के लक्ष्य के करीब, लेकिन कितना? दूसरे रोल पर अपने विकल्पों के बारे में सोचने का सबसे आसान तरीका है:
   • यदि दूसरा टॉस एक सिक्का है, तो हम शुरुआत में वापस आ जाएंगे।
   • अगर दूसरी बार भी एक कप है, तो हम कर रहे हैं!
5. जानें कि दोनों घटनाओं की दो घटनाओं की संभावना की गणना कैसे करें। अब हम जानते हैं कि आपके पास 50% मौका है कि आप एक कप फेंक देंगे, लेकिन क्या मौका है कि आप लगातार दो बार एक कप फेंकेंगे? इस संभावना की गणना करने के लिए, दोनों की संभावना को गुणा करें। इस मामले में यह 0.5 x 0.5 = 0.25 है। बेशक, यह भी मौका है कि आप सिर को रोल करेंगे और फिर पूंछ करेंगे, क्योंकि उनके पास 0.5 होने का मौका है: 0.5 x 0.5 = 0.25।
6. समीकरण के लिए "सिर, फिर पूंछ" के लिए परिणाम जोड़ें। अब जब हमने इस घटना की संभावना की गणना कर ली है, तो हम समीकरण का विस्तार करने के लिए आगे बढ़ सकते हैं। एक 0.25 (या 1/4) मौका है कि हम आगे बढ़ने के बिना दो बार फेंकने को बेकार कर देंगे। लेकिन अब भी हमें औसत परिणाम प्राप्त करने के लिए औसतन अधिक संख्या में एक्स थ्रो की आवश्यकता है, साथ ही 2 जो हमने पहले ही फेंक दिया है। समीकरण रूप में, यह (0.25) (x + 2) बन जाता है, जिसे अब हम समीकरण में जोड़ सकते हैं:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + ___
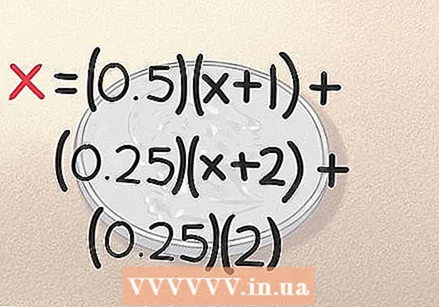7. समीकरण के लिए "हेडिंग, हेडिंग" के लिए परिणाम जोड़ें। यदि आप सिक्कों के पहले दो टॉस के साथ सिर, सिर को रोल करते हैं, तो आप कर रहे हैं। आपको इसका परिणाम बिलकुल 2 फेंक में मिला। जैसा कि हमने पहले उल्लेख किया, ऐसा होने का 0.25 मौका है, इसलिए इसके लिए समीकरण (0.25) (2) है। हमारी तुलना अब पूरी हो गई है:
   • x = (0.5) (x + 1) + (0.25) (x + 2) + (0.25) (2)
   • यदि आप सुनिश्चित नहीं हैं कि आपने हर संभव स्थिति के माध्यम से सोचा है, तो यह जांचने का एक आसान तरीका है कि समीकरण पूरा हो गया है। समीकरण के प्रत्येक भाग में पहली संख्या इस संभावना का प्रतिनिधित्व करती है कि एक घटना घटित होगी। यह हमेशा 1 तक जोड़ेगा। यहां, 0.5 + 0.25 + 0.25 = 1 है, इसलिए हम जानते हैं कि हमने हर स्थिति को शामिल किया है।
8. समीकरण को सरल कीजिए। चलिए गुणा करके समीकरण को थोड़ा आसान बनाते हैं। याद रखें, यदि आप कोष्ठकों में कुछ इस तरह देखते हैं: (0.5) (x + 1), तो आप प्रत्येक शब्द से 0.5 गुणा करते हैं जो कोष्ठकों के दूसरे सेट में है। यह आपको निम्नलिखित देता है: 0.5x + (0.5) (1), या 0.5x + 0.5। आइए समीकरण में प्रत्येक पद के लिए ऐसा करें, फिर इन शब्दों को संयोजित करें ताकि यह सब थोड़ा सरल दिखाई दे:
   • x = 0.5x + (0.5) (1) + 0.25x + (0.25) (2) + (0.25) (2)
   • x = 0.5x + 0.5 + 0.25x + 0.5 + 0.5
   • x = 0.75x + 1.5
9. X के लिए हल करें। किसी भी समीकरण में, आपको गणना करने के लिए समीकरण के एक तरफ x को अलग करना होगा। याद रखें, x का अर्थ है "एक पंक्ति में दो बार सिर पाने के लिए आपके द्वारा सिक्कों की औसत संख्या।" जब हमने एक्स की गणना की है, तो हमने अपना उत्तर भी ढूंढ लिया है।
   • x = 0.75x + 1.5
   • x - 0.75x = 0.75x + 1.5 - 0.75x
   • 0.25x = 1.5
   • (0.25x) / (0.25) = (1.5) / (0.25)
   • x = 6
   • औसतन, आपको दो बार सिर फेंकने से पहले 6 बार एक सिक्का उछालना होगा।

3 की विधि 3: अवधारणा को समझें

1. वास्तव में अपेक्षित मूल्य क्या है। अपेक्षा मूल्य सबसे स्पष्ट या तार्किक परिणाम जरूरी नहीं है। कभी-कभी एक दी गई स्थिति में एक उम्मीद का मूल्य भी एक असंभव मूल्य हो सकता है। उदाहरण के लिए, किसी गेम के लिए € 10 से अधिक के पुरस्कार के साथ उम्मीद का मूल्य + € 5 हो सकता है। अपेक्षा मूल्य क्या इंगित करता है कि किसी विशेष घटना का कितना मूल्य है। यदि किसी गेम का अनुमानित मूल्य + € 5 है, तो आप इसे खेल सकते हैं यदि आपको लगता है कि यह समय और पैसे के लायक है तो आप प्रति गेम प्राप्त कर सकते हैं। यदि किसी अन्य गेम का अपेक्षित मूल्य है - $ 20, तो आप इसे केवल तभी खेलते हैं जब आपको लगता है कि प्रत्येक गेम की कीमत $ 20 है।
2. स्वतंत्र घटनाओं की अवधारणा को समझें। रोजमर्रा की जिंदगी में, हम में से बहुत से लोग सोचते हैं कि हमारे पास एक भाग्यशाली दिन है जब कुछ अच्छी चीजें होती हैं, और हम बाकी के दिन इस तरह से जाने की उम्मीद करते हैं।उसी तरह, हम सोच सकते हैं कि हमारे पास एक दुर्घटना हुई है और वास्तव में अब कुछ मजेदार करने की जरूरत है। गणितीय रूप से, चीजें इस तरह से नहीं जाती हैं। यदि आप एक नियमित सिक्का फेंकते हैं, तो ठीक वही मौका है कि आप एक सिर या एक सिक्का फेंक देंगे। इससे कोई फर्क नहीं पड़ता कि आपने कितनी बार फेंका है; अगली बार जब आप इसे फेंकेंगे तब भी यह उसी तरह काम करेगा। सिक्का टॉस अन्य टॉस के "स्वतंत्र" है, यह इससे प्रभावित नहीं है।
   • यह विश्वास कि आप सिक्के फेंकते समय भाग्यशाली या अशुभ हो सकते हैं (या संयोग का कोई अन्य खेल), या तथ्य यह है कि आपके सभी बुरे भाग्य अब समाप्त हो गए हैं और भाग्य आपके पक्ष में है जिसे जुआरी धोखा (या जुआरी की पतनशीलता) भी कहा जाता है। यह जोखिम भरा या मूर्खतापूर्ण निर्णय लेने के लिए लोगों की प्रवृत्ति के साथ करना पड़ता है जब उन्हें लगता है कि भाग्य उनके पक्ष में है, या यदि वे "भाग्यशाली लकीर" महसूस करते हैं या यदि उन्हें लगता है कि उनकी "किस्मत पलटने वाली है।"
3. बड़ी संख्या के कानून को समझें। आप सोच सकते हैं कि उम्मीद का मूल्य वास्तव में उपयोगी नहीं है, क्योंकि यह केवल आपको शायद ही कभी बताता है कि किसी स्थिति का वास्तविक परिणाम क्या है। यदि आपने गणना की है कि रूलेट गेम का अपेक्षित मूल्य है - € 1, और आप 3 बार गेम खेलते हैं, तो आप आमतौर पर - € 10, या + € 60, या कुछ अन्य परिणाम के साथ समाप्त होंगे। "बिग नंबर्स का कानून" यह समझाने में मदद करता है कि अपेक्षा मूल्य अधिक उपयोगी क्यों है जितना आप सोच सकते हैं: जितना अधिक आप खेलते हैं, अपेक्षा मूल्य के करीब औसत परिणाम होगा। जब आप बड़ी संख्या में घटनाओं को देखते हैं, तो एक अच्छा मौका है कि अंतिम परिणाम अपेक्षित मूल्य के करीब है।

टिप्स

• उन स्थितियों के लिए जहां कई परिणाम संभव हैं, आप परिणामों और उनकी संभावनाओं का उपयोग करके अपेक्षित मूल्य की गणना करने के लिए कंप्यूटर में एक स्प्रेडशीट बना सकते हैं।
• ऊपर की € गणना अन्य मुद्राओं में भी काम करती है।

नेसेसिटीज़

• पेंसिल
• कागज़
• कैलकुलेटर