विषय

• कदम
• विधि 1 का 3: एक स्थिर पद के बिना घन समीकरण को कैसे हल करें
• विधि 2 का 3: गुणक का उपयोग करके संपूर्ण जड़ कैसे खोजें
• विधि 3 का 3: विभेदक का उपयोग करके एक समीकरण को कैसे हल करें

एक घन समीकरण में, उच्चतम घातांक 3 होता है, ऐसे समीकरण के 3 मूल (समाधान) होते हैं और इसका रूप होता है ${ डिस्प्लेस्टाइल कुल्हाड़ी ^ {3} + बीएक्स ^ {2} + सीएक्स + डी = 0}$... कुछ घन समीकरणों को हल करना इतना आसान नहीं है, लेकिन यदि आप सही विधि (अच्छी सैद्धांतिक पृष्ठभूमि के साथ) लागू करते हैं, तो आप सबसे जटिल घन समीकरण की जड़ों को भी ढूंढ सकते हैं - इसके लिए द्विघात समीकरण को हल करने के लिए सूत्र का उपयोग करें, खोजें पूरी जड़ें, या विवेचक की गणना करें।

कदम

विधि 1 का 3: एक स्थिर पद के बिना घन समीकरण को कैसे हल करें

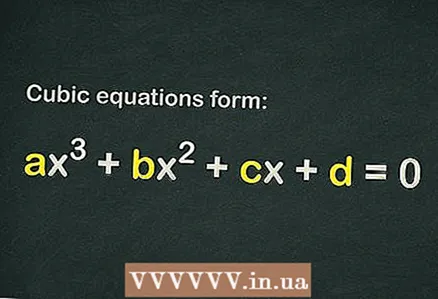1. 1 पता लगाएँ कि क्या घन समीकरण में एक मुक्त पद है डी{ डिस्प्लेस्टाइल डी}. घन समीकरण का रूप है ${ डिस्प्लेस्टाइल कुल्हाड़ी ^ {3} + बीएक्स ^ {2} + सीएक्स + डी = 0}$... किसी समीकरण को घन माने जाने के लिए, यह पर्याप्त है कि केवल पद ${ डिस्प्लेस्टाइल x ^ {3}}$ (अर्थात, कोई अन्य सदस्य बिल्कुल भी नहीं हो सकता है)।
   • यदि समीकरण का एक मुक्त पद है ${ डिस्प्लेस्टाइल डी}$, एक अलग विधि का उपयोग करें।
   • यदि समीकरण में ${ डिस्प्लेस्टाइल ए = 0}$, यह घन नहीं है।
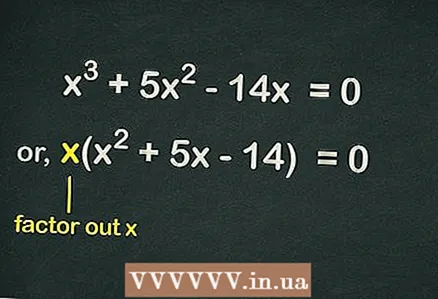2. 2 कोष्ठक से बाहर निकालें एक्स{ डिस्प्लेस्टाइल x}. चूँकि समीकरण में कोई मुक्त पद नहीं है, समीकरण के प्रत्येक पद में चर शामिल है ${ डिस्प्लेस्टाइल x}$... इसका मतलब है कि एक ${ डिस्प्लेस्टाइल x}$ समीकरण को सरल बनाने के लिए कोष्ठक से बाहर रखा जा सकता है। इस प्रकार, समीकरण इस प्रकार लिखा जाएगा: ${ डिस्प्लेस्टाइल एक्स (कुल्हाड़ी ^ {2} + बीएक्स + सी)}$.
   • उदाहरण के लिए, एक घन समीकरण दिया गया है ${ डिस्प्लेस्टाइल 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • साथ ले जाएं ${ डिस्प्लेस्टाइल x}$ कोष्ठक और प्राप्त करें ${ डिस्प्लेस्टाइल x (3x ^ {2} -2x + 14) = 0}$
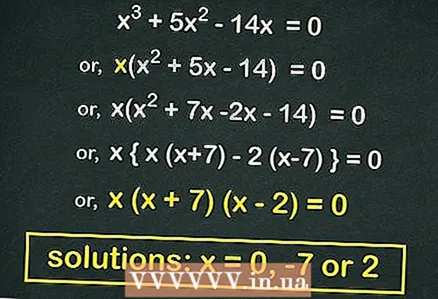3. 3 गुणनखंड (दो द्विपदों का गुणनफल) द्विघात समीकरण (यदि संभव हो)। फॉर्म के कई द्विघात समीकरण ${ डिस्प्लेस्टाइल कुल्हाड़ी ^ {2} + बीएक्स + सी = 0}$ गुणनखंडित किया जा सकता है। ऐसा समीकरण निकलेगा यदि हम निकाल दें ${ डिस्प्लेस्टाइल x}$ कोष्ठक के बाहर। हमारे उदाहरण में:
   • कोष्ठक से बाहर निकालें ${ डिस्प्लेस्टाइल x}$: ${ डिस्प्लेस्टाइल x (x ^ {2} + 5x-14) = 0}$
   • द्विघात समीकरण का गुणनखंड करें: ${ डिस्प्लेस्टाइल x (x + 7) (x-2) = 0}$
   • प्रत्येक बिन की बराबरी करें ${ डिस्प्लेस्टाइल 0}$... इस समीकरण की जड़ें हैं ${ डिस्प्लेस्टाइल x = 0, x = -7, x = 2}$.
4. 4 एक विशेष सूत्र का उपयोग करके द्विघात समीकरण को हल करें। ऐसा करें यदि द्विघात समीकरण को गुणनखंडित नहीं किया जा सकता है। किसी समीकरण के दो मूल ज्ञात करने के लिए, गुणांकों के मान ${ डिस्प्लेस्टाइल ए}$, ${ डिस्प्लेस्टाइल बी}$, ${ डिस्प्लेस्टाइल सी}$ सूत्र में स्थानापन्न ${ डिस्प्लेस्टाइल { फ्रैक {-बी अपराह्न { sqrt {बी ^ {2} -4ac}}} {2a}}}$.
   • हमारे उदाहरण में, गुणांक के मूल्यों को प्रतिस्थापित करें ${ डिस्प्लेस्टाइल ए}$, ${ डिस्प्लेस्टाइल बी}$, ${ डिस्प्लेस्टाइल सी}$ (${ डिस्प्लेस्टाइल 3}$, ${ डिस्प्लेस्टाइल -2}$, ${ डिस्प्लेस्टाइल 14}$) सूत्र में:

     ${ डिस्प्लेस्टाइल { फ्रैक {-बी अपराह्न { sqrt {बी ^ {2} -4ac}}} {2a}}}$

     ${ डिस्प्लेस्टाइल { फ्रैक {- (- 2) अपराह्न { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ डिस्प्लेस्टाइल { फ्रैक {2 अपराह्न { sqrt {4- (12) (14)}}} {6}}}$

     ${ डिस्प्लेस्टाइल { फ्रैक {2 अपराह्न { sqrt {(4-168}}} {6}}}$

     ${ डिस्प्लेस्टाइल { फ्रैक {2 अपराह्न { sqrt {-164}}} {6}}}$

   • पहली जड़:

     ${ डिस्प्लेस्टाइल { फ्रैक {2 + { sqrt {-164}}} {6}}}$

     ${ डिस्प्लेस्टाइल { फ्रैक {2 + 12,8i} {6}}}$

   • दूसरी जड़:

     ${ प्रदर्शन शैली { फ़्रेक {2-12,8i} {6}}}$

5. 5 घन समीकरण के समाधान के रूप में शून्य और द्विघात जड़ों का प्रयोग करें। द्विघात समीकरणों की दो जड़ें होती हैं, जबकि घन की तीन होती हैं। आप पहले ही दो हल खोज चुके हैं - ये द्विघात समीकरण के मूल हैं। यदि आप कोष्ठक के बाहर "x" लगाते हैं, तो तीसरा समाधान होगा ${ डिस्प्लेस्टाइल 0}$.
   • यदि आप कोष्ठक में से "x" निकालते हैं, तो आपको मिलता है ${ डिस्प्लेस्टाइल एक्स (कुल्हाड़ी ^ {2} + बीएक्स + सी) = 0}$, अर्थात्, दो कारक: ${ डिस्प्लेस्टाइल x}$ और कोष्ठक में द्विघात समीकरण। यदि इनमें से कोई भी कारक ${ डिस्प्लेस्टाइल 0}$, संपूर्ण समीकरण भी के बराबर है ${ डिस्प्लेस्टाइल 0}$.
   • इस प्रकार, द्विघात समीकरण के दो मूल घन समीकरण के हल होते हैं। तीसरा उपाय है ${ डिस्प्लेस्टाइल x = 0}$.

विधि 2 का 3: गुणक का उपयोग करके संपूर्ण जड़ कैसे खोजें

1. 1 सुनिश्चित करें कि घन समीकरण में एक मुक्त पद है डी{ डिस्प्लेस्टाइल डी}. यदि फॉर्म के समीकरण में ${ डिस्प्लेस्टाइल कुल्हाड़ी ^ {3} + बीएक्स ^ {2} + सीएक्स + डी = 0}$ एक स्वतंत्र सदस्य है ${ डिस्प्लेस्टाइल डी}$ (जो शून्य के बराबर नहीं है), कोष्ठक के बाहर "x" लगाने से काम नहीं चलेगा। इस मामले में, इस खंड में उल्लिखित विधि का उपयोग करें।
   • उदाहरण के लिए, एक घन समीकरण दिया गया है ${ डिस्प्लेस्टाइल 2x ^ {3} + 9x ^ {2} + 13x = -6}$... समीकरण के दाईं ओर शून्य प्राप्त करने के लिए, जोड़ें ${ डिस्प्लेस्टाइल 6}$ समीकरण के दोनों ओर।
   • समीकरण बन जाएगा ${ डिस्प्लेस्टाइल 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... जैसा ${ डिस्प्लेस्टाइल डी = 6}$, पहले खंड में वर्णित विधि का उपयोग नहीं किया जा सकता है।
2. 2 गुणांक के कारकों को लिखिए ए{ डिस्प्लेस्टाइल ए} और एक स्वतंत्र सदस्य डी{ डिस्प्लेस्टाइल डी}. अर्थात्, संख्या के गुणनखंड ज्ञात कीजिए ${ डिस्प्लेस्टाइल x ^ {3}}$ और समान चिह्न से पहले की संख्याएँ। याद रखें कि किसी संख्या के गुणनखंड वे संख्याएँ होती हैं, जिन्हें गुणा करने पर वह संख्या प्राप्त होती है।
   • उदाहरण के लिए, संख्या प्राप्त करने के लिए 6, आपको गुणा करना होगा ${ डिस्प्लेस्टाइल 6 बार 1}$ तथा ${ डिस्प्लेस्टाइल 2 बार 3}$... तो संख्या 1, 2, 3, 6 संख्या के कारक हैं 6.
   • हमारे समीकरण में ${ डिस्प्लेस्टाइल ए = 2}$ तथा ${ डिस्प्लेस्टाइल डी = 6}$... मल्टीप्लायरों 2 हैं 1 तथा 2... मल्टीप्लायरों 6 नंबर हैं 1, 2, 3 तथा 6.
3. 3 प्रत्येक कारक को विभाजित करें ए{ डिस्प्लेस्टाइल ए} प्रत्येक कारक के लिए डी{ डिस्प्लेस्टाइल डी}. परिणामस्वरूप, आपको बहुत से भिन्न और कई पूर्णांक मिलते हैं; घन समीकरण का मूल पूर्णांकों में से एक होगा या पूर्णांकों में से किसी एक का ऋणात्मक मान होगा।
   • हमारे उदाहरण में, कारकों को विभाजित करें ${ डिस्प्लेस्टाइल ए}$ (1 तथा 2) कारकों द्वारा ${ डिस्प्लेस्टाइल डी}$ (1, 2, 3 तथा 6) आपको मिलेगा: ${ डिस्प्लेस्टाइल 1}$, ${ डिस्प्लेस्टाइल { फ्रैक {1} {2}}}$, ${ प्रदर्शन शैली { फ़्रेक {1} {3}}}$, ${ प्रदर्शन शैली { फ़्रेक {1} {6}}}$, ${ डिस्प्लेस्टाइल 2}$ तथा ${ डिस्प्लेस्टाइल { फ्रैक {2} {3}}}$... अब इस सूची में प्राप्त भिन्नों और संख्याओं के ऋणात्मक मान जोड़ें: ${ डिस्प्लेस्टाइल 1}$, ${ डिस्प्लेस्टाइल -1}$, ${ प्रदर्शन शैली { फ़्रेक {1} {2}}}$, ${ डिस्प्लेस्टाइल - { फ्रैक {1} {2}}}$, ${ प्रदर्शन शैली { फ़्रेक {1} {3}}}$, ${ डिस्प्लेस्टाइल - { फ्रैक {1} {3}}}$, ${ प्रदर्शन शैली { फ़्रेक {1} {6}}}$, ${ प्रदर्शन शैली - { फ़्रेक {1} {6}}}$, ${ डिस्प्लेस्टाइल 2}$, ${ डिस्प्लेस्टाइल -2}$, ${ डिस्प्लेस्टाइल { फ्रैक {2} {3}}}$ तथा ${ डिस्प्लेस्टाइल - { फ्रैक {2} {3}}}$... घन समीकरण के पूरे मूल इस सूची से कुछ संख्याएँ हैं।
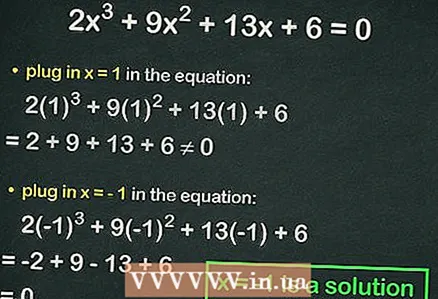4. 4 घन समीकरण में पूर्णांकों को प्लग करें। यदि समानता सत्य है, तो प्रतिस्थापित संख्या समीकरण का मूल है। उदाहरण के लिए, समीकरण में स्थानापन्न करें ${ डिस्प्लेस्टाइल 1}$:
   • ${ डिस्प्लेस्टाइल 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ डिस्प्लेस्टाइल 2 + 9 + 13 + 6}$ 0, यानी समानता नहीं देखी जाती है। इस मामले में, अगले नंबर में प्लग करें।
   • विकल्प ${ डिस्प्लेस्टाइल -1}$: ${ डिस्प्लेस्टाइल (-2) +9 + (- 13) +6}$ = 0. इस प्रकार, ${ डिस्प्लेस्टाइल -1}$ समीकरण की पूरी जड़ है।
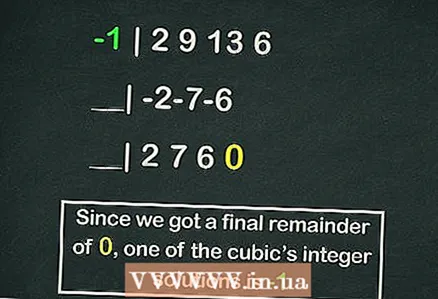5. 5 बहुपदों को विभाजित करने की विधि का प्रयोग करें हॉर्नर की योजनासमीकरण की जड़ों को तेजी से खोजने के लिए। ऐसा करें यदि आप समीकरण में संख्याओं को मैन्युअल रूप से प्रतिस्थापित नहीं करना चाहते हैं। हॉर्नर की योजना में, पूर्णांकों को समीकरण के गुणांकों के मानों से विभाजित किया जाता है ${ डिस्प्लेस्टाइल ए}$, ${ डिस्प्लेस्टाइल बी}$, ${ डिस्प्लेस्टाइल सी}$ तथा ${ डिस्प्लेस्टाइल डी}$... यदि संख्याएँ समान रूप से विभाज्य हैं (अर्थात, शेषफल है ${ डिस्प्लेस्टाइल 0}$), एक पूर्णांक समीकरण का मूल है।
   • हॉर्नर की योजना एक अलग लेख के योग्य है, लेकिन निम्नलिखित इस योजना का उपयोग करके हमारे घन समीकरण की जड़ों में से एक की गणना करने का एक उदाहरण है:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • तो शेष है ${ डिस्प्लेस्टाइल 0}$, लेकिन ${ डिस्प्लेस्टाइल -1}$ समीकरण की जड़ों में से एक है।

विधि 3 का 3: विभेदक का उपयोग करके एक समीकरण को कैसे हल करें

1. 1 समीकरण के गुणांकों के मान लिखिए ए{ डिस्प्लेस्टाइल ए}, बी{ डिस्प्लेस्टाइल बी}, सी{ डिस्प्लेस्टाइल सी} तथा डी{ डिस्प्लेस्टाइल डी}. हम अनुशंसा करते हैं कि आप संकेतित गुणांकों के मूल्यों को पहले से लिख लें ताकि भविष्य में भ्रमित न हों।
   • उदाहरण के लिए, समीकरण दिया गया है ${ डिस्प्लेस्टाइल x ^ {3} -3x ^ {2} + 3x-1}$... लिखो ${ डिस्प्लेस्टाइल ए = 1}$, ${ डिस्प्लेस्टाइल बी = -3}$, ${ डिस्प्लेस्टाइल सी = 3}$ तथा ${ डिस्प्लेस्टाइल डी = -1}$... याद करें कि यदि पहले ${ डिस्प्लेस्टाइल x}$ कोई संख्या नहीं है, संबंधित गुणांक अभी भी मौजूद है और बराबर है ${ डिस्प्लेस्टाइल 1}$.
2. 2 एक विशेष सूत्र का उपयोग करके शून्य विवेचक की गणना करें। विभेदक का उपयोग करके एक घन समीकरण को हल करने के लिए, आपको कई कठिन गणना करने की आवश्यकता होती है, लेकिन यदि आप सभी चरणों को सही ढंग से करते हैं, तो यह विधि सबसे जटिल घन समीकरणों को हल करने के लिए अनिवार्य हो जाएगी। पहली गणना ${ डिस्प्लेस्टाइल डेल्टा _ {0}}$ (शून्य विभेदक) पहला मूल्य है जिसकी हमें आवश्यकता है; ऐसा करने के लिए, सूत्र में संबंधित मानों को प्रतिस्थापित करें ${ डिस्प्लेस्टाइल डेल्टा _ {0} = बी ^ {2} -3ac}$.
   • विभेदक एक संख्या है जो एक बहुपद की जड़ों की विशेषता है (उदाहरण के लिए, द्विघात समीकरण के विवेचक की गणना सूत्र द्वारा की जाती है) ${ डिस्प्लेस्टाइल बी ^ {2} -4ac}$).
   • हमारे समीकरण में:

     ${ डिस्प्लेस्टाइल बी ^ {2} -3ac}$

     ${ डिस्प्लेस्टाइल (-3) ^ {2} -3 (1) (3)}$

     ${ डिस्प्लेस्टाइल 9-3 (1) (3)}$

     ${ डिस्प्लेस्टाइल 9-9 = 0 = डेल्टा _ {0}}$

3. 3 सूत्र का उपयोग करके पहले विवेचक की गणना करें Δ1=2बी3−9एबीसी+27ए2डी{ डिस्प्लेस्टाइल डेल्टा _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. पहला विभेदक ${ डिस्प्लेस्टाइल डेल्टा _ {1}}$ - यह दूसरा महत्वपूर्ण मूल्य है; इसकी गणना करने के लिए, संबंधित मानों को निर्दिष्ट सूत्र में प्लग करें।
   • हमारे समीकरण में:

     ${ डिस्प्लेस्टाइल 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ डिस्प्लेस्टाइल 2 (-27) -9 (-9) +27 (-1)}$

     ${ डिस्प्लेस्टाइल -54 + 81-27}$

     ${ डिस्प्लेस्टाइल 81-81 = 0 = डेल्टा _ {1}}$

4. 4 गणना करें:${ डिस्प्लेस्टाइल डेल्टा = ( डेल्टा _ {1} ^ {2} -4 डेल्टा _ {0} ^ {3}) div -27a ^ {2}}$... अर्थात्, प्राप्त मानों के माध्यम से घन समीकरण का विवेचक ज्ञात कीजिए ${ डिस्प्लेस्टाइल डेल्टा _ {0}}$ तथा ${ डिस्प्लेस्टाइल डेल्टा _ {1}}$... यदि एक घन समीकरण का विभेदक धनात्मक है, तो समीकरण के तीन मूल हैं; यदि विवेचक शून्य है, तो समीकरण के एक या दो मूल हैं; यदि विवेचक ऋणात्मक है, तो समीकरण का एक मूल है।
   • एक घन समीकरण में हमेशा कम से कम एक मूल होता है, क्योंकि इस समीकरण का ग्राफ कम से कम एक बिंदु पर X-अक्ष को काटता है।
   • हमारे समीकरण में ${ डिस्प्लेस्टाइल डेल्टा _ {0}}$ तथा ${ डिस्प्लेस्टाइल डेल्टा _ {1}}$ बराबर हैं ${ डिस्प्लेस्टाइल 0}$, ताकि आप आसानी से गणना कर सकें ${ डिस्प्लेस्टाइल डेल्टा}$:

     ${ डिस्प्लेस्टाइल ( डेल्टा _ {1} ^ {2} -4 डेल्टा _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ डिस्प्लेस्टाइल ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ डिस्प्लेस्टाइल 0-0 div 27}$

     ${ डिस्प्लेस्टाइल 0 = डेल्टा}$... इस प्रकार, हमारे समीकरण के एक या दो मूल हैं।

5. 5 गणना करें:${ डिस्प्लेस्टाइल सी = ^ {3} { वर्ग { बाएं ({ वर्ग { डेल्टा _ {1} ^ {2} -4 डेल्टा _ {0} ^ {3}}} + डेल्टा _ {1 } दाएँ) div 2}}}$. ${ डिस्प्लेस्टाइल सी}$ - यह पाया जाने वाला अंतिम महत्वपूर्ण मात्रा है; यह आपको समीकरण की जड़ों की गणना करने में मदद करेगा। मानों को निर्दिष्ट सूत्र में बदलें ${ डिस्प्लेस्टाइल डेल्टा _ {1}}$ तथा ${ डिस्प्लेस्टाइल डेल्टा _ {0}}$.
   • हमारे समीकरण में:

     ${ डिस्प्लेस्टाइल ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ डिस्प्लेस्टाइल ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ डिस्प्लेस्टाइल ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ डिस्प्लेस्टाइल 0 = सी}$

6. 6 समीकरण के तीन मूल ज्ञात कीजिए। इसे सूत्र के साथ करें ${ डिस्प्लेस्टाइल - (बी + यू ^ {एन} सी + डेल्टा _ {0} डिव (यू ^ {एन} सी)) डिव 3 ए}$, कहाँ पे ${ डिस्प्लेस्टाइल यू = (- 1 + { sqrt {-3}}) div 2}$, लेकिन एन के बराबर है 1, 2 या 3... इस सूत्र में उपयुक्त मानों को प्रतिस्थापित करें - परिणामस्वरूप, आपको समीकरण के तीन मूल प्राप्त होंगे।
   • सूत्र का उपयोग करके मान की गणना करें एन = 1, 2 या 3और फिर उत्तर की जाँच करें। यदि आप अपने उत्तर की जांच करते समय 0 प्राप्त करते हैं, तो यह मान समीकरण का मूल है।
   • हमारे उदाहरण में, स्थानापन्न 1 में ${ डिस्प्लेस्टाइल x ^ {3} -3x ^ {2} + 3x-1}$ और पाओ 0, अर्थात 1 समीकरण की जड़ों में से एक है।