विषय

• कदम
• विधि 1 में से 4: गुणकों की एक श्रृंखला
• विधि 2 का 4: प्राइम फैक्टरिंग
• विधि 3 का 4: सामान्य भाजक ढूँढना
• विधि 4 का 4: यूक्लिड का एल्गोरिथम
• टिप्स

एक बहु एक ऐसी संख्या है जो किसी दी गई संख्या से समान रूप से विभाज्य होती है।संख्याओं के समूह का लघुत्तम समापवर्त्य (LCM) वह छोटी से छोटी संख्या है जो समूह में प्रत्येक संख्या से समान रूप से विभाज्य होती है। कम से कम सामान्य गुणक खोजने के लिए, आपको दी गई संख्याओं के अभाज्य गुणनखंड ज्ञात करने होंगे। एलसीएम की गणना कई अन्य विधियों का उपयोग करके भी की जा सकती है जो दो या दो से अधिक संख्याओं के समूहों पर लागू होती हैं।

कदम

विधि 1 में से 4: गुणकों की एक श्रृंखला

1. 1 दिए गए नंबरों को देखें। यहां वर्णित विधि का सबसे अच्छा उपयोग तब किया जाता है जब दो संख्याएँ दी जाती हैं, जिनमें से प्रत्येक 10 से कम होती है। यदि संख्याएँ बड़ी हैं, तो एक अलग विधि का उपयोग करें।
   • उदाहरण के लिए, 5 और 8 का लघुत्तम समापवर्तक ज्ञात कीजिए। ये छोटी संख्याएँ हैं, इसलिए आप इस विधि का उपयोग कर सकते हैं।
2. 2 संख्याओं की एक श्रृंखला लिखिए जो पहली संख्या के गुणज हों। एक बहु एक ऐसी संख्या है जो किसी दी गई संख्या से समान रूप से विभाज्य होती है। गुणन तालिका में कई संख्याएँ पाई जा सकती हैं।
   • उदाहरण के लिए, जो संख्याएँ 5 के गुणज हैं वे हैं: 5, 10, 15, 20, 25, 30, 35, 40।
3. 3 संख्याओं की एक श्रृंखला लिखिए जो पहली संख्या के गुणज हों। संख्याओं की दो पंक्तियों की तुलना करने के लिए पहली संख्या के गुणकों के तहत ऐसा करें।
   • उदाहरण के लिए, जो संख्याएँ 8 के गुणज हैं वे हैं: 8, 16, 24, 32, 40, 48, 56 और 64।
4. 4 गुणज की दोनों पंक्तियों में दिखाई देने वाली सबसे छोटी संख्या ज्ञात कीजिए। कुल ज्ञात करने के लिए आपको गुणकों की लंबी श्रंखला लिखनी पड़ सकती है। गुणज की दोनों पंक्तियों में दिखाई देने वाली सबसे छोटी संख्या सबसे छोटी सामान्य गुणज होती है।
   • उदाहरण के लिए, 5 और 8 के गुणकों की श्रृंखला में दिखाई देने वाली सबसे छोटी संख्या 40 है। इसलिए, 40, 5 और 8 का सबसे छोटा सामान्य गुणज है।

विधि 2 का 4: प्राइम फैक्टरिंग

1. 1 दिए गए नंबरों को देखें। यहां वर्णित विधि का सबसे अच्छा उपयोग तब किया जाता है जब दो संख्याएँ दी जाती हैं, जिनमें से प्रत्येक 10 से बड़ी होती है। यदि दी गई संख्याएँ छोटी हैं, तो एक अलग विधि का उपयोग करें।
   • उदाहरण के लिए, 20 और 84 का सबसे छोटा सामान्य गुणक ज्ञात कीजिए। प्रत्येक संख्या 10 से बड़ी है, इसलिए आप इस पद्धति का उपयोग कर सकते हैं।
2. 2 फैक्टर आउट पहला नंबर। यानी आपको ऐसी अभाज्य संख्याएँ ज्ञात करनी होंगी, जिन्हें गुणा करने पर आपको दी गई संख्या प्राप्त हो। एक बार जब आप प्रमुख कारकों को ढूंढ लेते हैं, तो उन्हें समानता के रूप में लिख लें।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल गणितबीएफ {2} गुना 10 = 20}$ तथा ${ डिस्प्लेस्टाइल mathbf {2} बार mathbf {5} = 10}$... इस प्रकार, 20 के अभाज्य गुणनखंड 2, 2 और 5 हैं। उन्हें व्यंजक के रूप में लिखिए: ${ डिस्प्लेस्टाइल 20 = 2 गुना 2 गुना 5}$.
3. 3 दूसरे नंबर को फैक्टर करें। इसे उसी तरह करें जैसे आपने पहली संख्या का गुणनखंड किया था, अर्थात अभाज्य संख्याएँ ज्ञात करें, जिन्हें गुणा करने पर दी गई संख्या प्राप्त होगी।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल mathbf {2} बार 42 = 84}$, ${ डिस्प्लेस्टाइल गणितबीएफ {7} बार 6 = 42}$ तथा ${ डिस्प्लेस्टाइल mathbf {3} बार mathbf {2} = 6}$... इस प्रकार, 84 के अभाज्य गुणनखंड 2, 7, 3 और 2 हैं। उन्हें एक व्यंजक के रूप में लिखिए: ${ डिस्प्लेस्टाइल ८४ = २ गुना ७ गुना ३ गुना २}$.
4. 4 दोनों संख्याओं के सामान्य गुणनखंड लिखिए। इन कारकों को गुणन के रूप में लिखिए। जैसा कि आप प्रत्येक कारक को लिखते हैं, इसे दोनों भावों में काट दें (व्यंजक जो अभाज्य गुणनखंडों का वर्णन करते हैं)।
   • उदाहरण के लिए, दोनों संख्याओं का उभयनिष्ठ गुणनखंड 2 है, इसलिए लिखिए ${ डिस्प्लेस्टाइल 2 बार}$ और दोनों भावों में 2 को काट दें।
   • दोनों संख्याओं का उभयनिष्ठ 2 का एक अन्य गुणनखंड है, इसलिए लिखिए ${ डिस्प्लेस्टाइल 2 बार 2}$ और दूसरे 2 को दोनों भावों में काट दें।
5. 5 गुणन संक्रिया में शेष गुणनखंडों को जोड़ें। ये ऐसे गुणनखंड हैं जिन्हें दोनों व्यंजकों में काट नहीं दिया जाता है, अर्थात ऐसे गुणनखंड जो दोनों संख्याओं के लिए उभयनिष्ठ नहीं हैं।
   • उदाहरण के लिए, अभिव्यक्ति में ${ डिस्प्लेस्टाइल 20 = 2 गुना 2 गुना 5}$ दोनों 2 (2) को काट दिया गया है क्योंकि वे सामान्य गुणनखंड हैं। गुणनखंड 5 को पार नहीं किया गया है, इसलिए गुणन संक्रिया को इस प्रकार लिखें: ${ डिस्प्लेस्टाइल 2 बार 2 बार 5}$
   • अभिव्यक्ति में ${ डिस्प्लेस्टाइल ८४ = २ गुना ७ गुना ३ गुना २}$ दोनों 2 को भी काट दिया गया है (2)। गुणनखंड 7 और 3 को क्रॉस आउट नहीं किया गया है, इसलिए गुणन संक्रिया को इस प्रकार लिखें: ${ डिस्प्लेस्टाइल 2 बार 2 बार 5 बार 7 बार 3}$.
6. 6 कम से कम सामान्य गुणक की गणना करें। ऐसा करने के लिए, दर्ज गुणन संक्रिया में संख्याओं को गुणा करें।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 2 बार 2 बार 5 बार 7 बार 3 = 420}$... अतः 20 और 84 का लघुत्तम समापवर्तक 420 है।

विधि 3 का 4: सामान्य भाजक ढूँढना

1. 1 टिक-टैक-टो गेम के लिए ग्रिड बनाएं। इस तरह के ग्रिड में दो समानांतर सीधी रेखाएँ होती हैं जो अन्य दो समानांतर सीधी रेखाओं के साथ (समकोण पर) प्रतिच्छेद करती हैं। यह तीन पंक्तियों और तीन स्तंभों के साथ समाप्त होगा (ग्रिड # चिह्न के समान है)। पहली पंक्ति और दूसरे कॉलम में पहली संख्या लिखें। पहली पंक्ति और तीसरे कॉलम में दूसरी संख्या लिखें।
   • उदाहरण के लिए, 18 और 30 का सबसे छोटा सामान्य गुणक खोजें। पहली पंक्ति और दूसरे कॉलम में 18 लिखें, और पहली पंक्ति और तीसरे कॉलम में 30 लिखें।
2. 2 दोनों संख्याओं का भाजक ज्ञात कीजिए। इसे पहली पंक्ति और पहले कॉलम पर लिखें। प्रमुख कारकों की तलाश करना बेहतर है, लेकिन यह कोई आवश्यकता नहीं है।
   • उदाहरण के लिए, 18 और 30 सम संख्याएँ हैं, इसलिए उनका उभयनिष्ठ भाजक 2 है। इसलिए पहली पंक्ति और पहले कॉलम में 2 लिखें।
3. 3 प्रत्येक संख्या को पहले भाजक से विभाजित करें। प्रत्येक भागफल को संगत संख्या के नीचे लिखिए। भागफल दो संख्याओं को विभाजित करने का परिणाम है।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 18 डिव 2 = 9}$इसलिए 9 अंडर 18 लिखें।
   • ${ डिस्प्लेस्टाइल 30 डिव 2 = 15}$इसलिए 15 अंडर 30 लिखें।
4. 4 दोनों भागफलों के लिए सामान्य भाजक ज्ञात कीजिए। यदि ऐसा कोई भाजक नहीं है, तो अगले दो चरणों को छोड़ दें। अन्यथा, भाजक को दूसरी पंक्ति और पहले कॉलम में लिखें।
   • उदाहरण के लिए, 9 और 15 3 से विभाज्य हैं, इसलिए दूसरी पंक्ति और पहले कॉलम में 3 लिखें।
5. 5 प्रत्येक भागफल को दूसरे गुणनखंड से विभाजित करें। प्रत्येक भाग के परिणाम को संबंधित भागफल के अंतर्गत लिखें।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 9 डिव 3 = 3}$इसलिए 3 अंडर 9 लिखें।
   • ${ डिस्प्लेस्टाइल 15 डिव 3 = 5}$इसलिए 5 अंडर 15 लिखें।
6. 6 यदि आवश्यक हो, अतिरिक्त कोशिकाओं के साथ ग्रिड को पूरक करें। वर्णित चरणों को तब तक दोहराएं जब तक कि भागफल में एक सामान्य भाजक न हो।
7. 7 ग्रिड के पहले कॉलम और आखिरी पंक्ति में संख्याओं को सर्कल करें। फिर चयनित संख्याओं को गुणन संक्रिया के रूप में लिखिए।
   • उदाहरण के लिए, संख्या २ और ३ पहले कॉलम में हैं, और संख्याएँ ३ और ५ अंतिम पंक्ति में हैं, इसलिए गुणन संक्रिया को इस प्रकार लिखें: ${ डिस्प्लेस्टाइल 2 गुना 3 गुना 3 गुना 5}$.
8. 8 संख्याओं के गुणन का परिणाम ज्ञात कीजिए। यह दी गई दो संख्याओं के सबसे छोटे सामान्य गुणज की गणना करेगा।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 2 गुना 3 गुना 3 गुना 5 = 90}$... अत: 18 और 30 का लघुत्तम समापवर्तक 90 है।

विधि 4 का 4: यूक्लिड का एल्गोरिथम

1. 1 डिवीजन ऑपरेशन से जुड़ी शब्दावली याद रखें। लाभांश वह संख्या है जिसे विभाजित किया जा रहा है। भाजक वह संख्या है जिससे भाग दिया जाता है। भागफल दो संख्याओं को विभाजित करने का परिणाम है। शेष वह संख्या है जो दो संख्याओं को विभाजित करने पर शेष रहती है।
   • उदाहरण के लिए, अभिव्यक्ति में ${ डिस्प्लेस्टाइल 15 डिव 6 = 2}$ ओस्ट। 3:
     15 लाभांश है
     6 भाजक है
     2 भागफल है
     3 शेष है।
2. 2 एक व्यंजक लिखिए जो शेष भाग का वर्णन करता है। अभिव्यक्ति: ${ प्रदर्शन शैली { पाठ {लाभांश}} = { पाठ {भाजक}} बार { पाठ {भागफल}} + { पाठ {शेष}}}$... इस व्यंजक का उपयोग यूक्लिड के एल्गोरिथ्म को लिखने और दो संख्याओं का सबसे बड़ा सामान्य भाजक खोजने के लिए किया जाएगा।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल १५ = ६ गुना २ + ३}$.
   • सबसे बड़ा सामान्य भाजक (जीसीडी) वह सबसे बड़ी संख्या है जिससे सभी दी गई संख्याएं विभाज्य होती हैं।
   • इस पद्धति में, आपको सबसे पहले सबसे बड़ा सामान्य गुणनखंड खोजने की जरूरत है और फिर सबसे कम सामान्य गुणक की गणना करें।
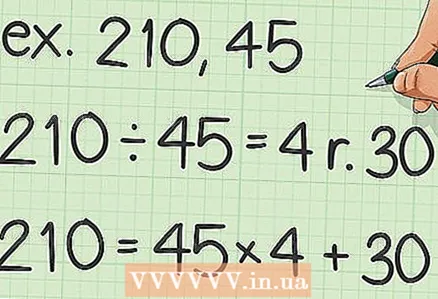3. 3 दो संख्याओं में से बड़ी संख्या को लाभांश के रूप में मानें। भाजक के रूप में दो संख्याओं में से छोटी संख्या पर विचार करें। इन संख्याओं के लिए, एक व्यंजक लिखिए जो शेष भाग का वर्णन करता है।
   • उदाहरण के लिए, 210 और 45 का लघुत्तम समापवर्तक ज्ञात कीजिए। यह व्यंजक लिखिए: ${ डिस्प्लेस्टाइल 210 = 45 बार 4 + 30}$.
4. 4 पहले भाजक को नए लाभांश में बदलें। शेष को नए भाजक के रूप में प्रयोग करें। इन संख्याओं के लिए, एक व्यंजक लिखिए जो शेष भाग का वर्णन करता है।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 45 = 30 बार 2 + 15}$.
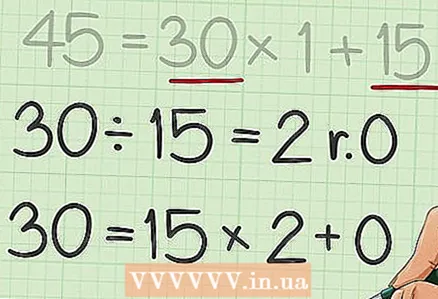5. 5 वर्णित चरणों को तब तक दोहराएं जब तक कि शेषफल 0 के बराबर न हो जाए। पिछले भाजक को नए लाभांश के रूप में और पिछले शेष को नए भाजक के रूप में उपयोग करें; इन संख्याओं के लिए उपयुक्त व्यंजक लिखिए।
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 30 = 15 बार 2 + 0}$... चूँकि शेषफल 0 है, आप आगे विभाजित नहीं कर सकते।
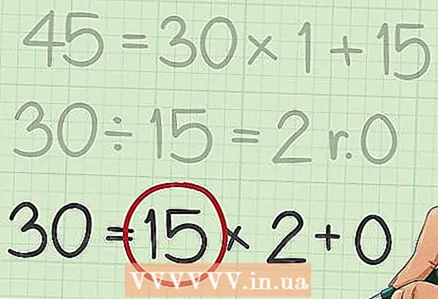6. 6 अंतिम भाजक को देखें। यह दो संख्याओं का सबसे बड़ा सामान्य भाजक है।
   • उदाहरण के लिए, अंतिम अभिव्यक्ति थी ${ डिस्प्लेस्टाइल 30 = 15 बार 2 + 0}$, इसलिए अंतिम भाजक 15 है। इसलिए 15 210 और 45 का सबसे बड़ा सामान्य भाजक है।
7. 7 दो संख्याओं को गुणा करें। फिर उत्पाद को सबसे बड़े सामान्य कारक से विभाजित करें। यह दो संख्याओं के लघुत्तम समापवर्त्य की गणना करेगा। [[[छवि: दो संख्याओं का लघुत्तम समापवर्त्य ज्ञात कीजिए चरण २५.webp | केंद्र]]
   • उदाहरण के लिए, ${ डिस्प्लेस्टाइल 210 बार 45 = 9450}$... परिणाम को GCD से विभाजित करें: ${ डिस्प्लेस्टाइल { फ्रैक {9450} {15}} = 630}$... अत: 630, 210 और 45 का लघुत्तम समापवर्त्य है।

टिप्स

• यदि आपको तीन या अधिक संख्याओं का एलसीएम ज्ञात करना है, तो इसे अपने लिए आसान बनाएं। उदाहरण के लिए, 16, 20 और 32 के एलसीएम को खोजने के लिए, पहले 16 और 20 (जो कि 80 है) का सबसे छोटा सामान्य गुणक खोजें, और फिर 80 और 32 का एलसीएम खोजें, जो कि 160 है।
• एलसीएम के कई उपयोग हैं। उदाहरण के लिए, भिन्नों को जोड़ने या घटाने के लिए, उनका हर समान होना चाहिए। यदि भिन्नों में अलग-अलग हर हैं, तो आपको भिन्नों को एक सामान्य हर में लाने के लिए बदलने की आवश्यकता है। और यह करना आसान है यदि आप सबसे छोटा सामान्य भाजक पाते हैं, जो कि भिन्नों के हर में मौजूद संख्याओं के सबसे छोटे सामान्य गुणक के बराबर है।