विषय

• कदम

त्रिकोणमितीय समीकरण में चर "x" (या कोई अन्य चर) के एक या अधिक त्रिकोणमितीय फलन होते हैं। एक त्रिकोणमितीय समीकरण को हल करना ऐसा मान "x" ढूंढ रहा है जो फ़ंक्शन (ओं) और पूरे समीकरण को संतुष्ट करता है।

• त्रिकोणमितीय समीकरणों के समाधान डिग्री या रेडियन में व्यक्त किए जाते हैं। उदाहरण:

एक्स = / 3; एक्स = 5π / 6; एक्स = 3π / 2; एक्स = 45 डिग्री; एक्स = ३७.१२ डिग्री; एक्स = 178.37 डिग्री।

• नोट: कोणों से त्रिकोणमितीय कार्यों के मान, रेडियन में व्यक्त किए गए, और कोणों से, डिग्री में व्यक्त किए गए, समान हैं। त्रिकोणमितीय कार्यों का वर्णन करने के साथ-साथ मूल त्रिकोणमितीय समीकरणों और असमानताओं के समाधान की शुद्धता की जांच करने के लिए एक के बराबर त्रिज्या वाले त्रिकोणमितीय सर्कल का उपयोग किया जाता है।
• त्रिकोणमितीय समीकरणों के उदाहरण:
  • पाप x + पाप 2x = 1/2; टीजी एक्स + सीटीजी एक्स = 1.732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1।

1. एक त्रिकोणमितीय वृत्त जिसकी त्रिज्या एक (इकाई वृत्त) है।
   • यह एक के बराबर त्रिज्या वाला एक वृत्त है और बिंदु O पर केंद्र है। यूनिट सर्कल चर "x" के 4 मूल त्रिकोणमितीय कार्यों का वर्णन करता है, जहां "x" एक्स अक्ष वामावर्त की सकारात्मक दिशा से मापा गया कोण है।
   • यदि "x" इकाई वृत्त पर कुछ कोण है, तो:
   • क्षैतिज अक्ष OAx फलन F (x) = cos x को परिभाषित करता है।
   • ऊर्ध्वाधर अक्ष OBy फलन F (x) = sin x को परिभाषित करता है।
   • ऊर्ध्वाधर अक्ष AT फलन F (x) = tan x को परिभाषित करता है।
   • क्षैतिज अक्ष BU फलन F (x) = ctg x को परिभाषित करता है।

• यूनिट सर्कल का उपयोग मूल त्रिकोणमितीय समीकरणों और असमानताओं को हल करने के लिए भी किया जाता है (इस पर "x" के विभिन्न पदों पर विचार किया जाता है)।

कदम

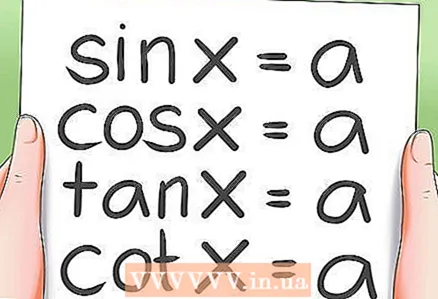1. 1 त्रिकोणमितीय समीकरणों को हल करने की अवधारणा।
   • त्रिकोणमितीय समीकरण को हल करने के लिए, इसे एक या अधिक मूल त्रिकोणमितीय समीकरणों में परिवर्तित करें। एक त्रिकोणमितीय समीकरण को हल करना अंततः चार बुनियादी त्रिकोणमितीय समीकरणों को हल करने के लिए नीचे आता है।
2. 2 मूल त्रिकोणमितीय समीकरणों को हल करना।
   • मूल त्रिकोणमितीय समीकरण 4 प्रकार के होते हैं:
   • पाप एक्स = ए; कॉस एक्स = ए
   • टीजी एक्स = ए; सीटीजी एक्स = ए
   • मूल त्रिकोणमितीय समीकरणों को हल करने में यूनिट सर्कल पर विभिन्न एक्स स्थितियों को देखना और रूपांतरण तालिका (या कैलकुलेटर) का उपयोग करना शामिल है।
   • उदाहरण 1. पाप x = 0.866। रूपांतरण तालिका (या कैलकुलेटर) का उपयोग करके, आपको उत्तर मिलता है: x = / ३। यूनिट सर्कल एक और जवाब देता है: 2π / 3। याद रखें: सभी त्रिकोणमितीय कार्य आवधिक होते हैं, अर्थात उनके मान दोहराए जाते हैं। उदाहरण के लिए, sin x और cos x की आवर्तता 2πn है, और tg x और ctg x की आवर्तता πn है। इसलिए, उत्तर इस प्रकार लिखा गया है:
   • x1 = / 3 + 2πn; x2 = 2π / 3 + 2πn।
   • उदाहरण 2.cos x = -1/2. रूपांतरण तालिका (या कैलकुलेटर) का उपयोग करके, आपको उत्तर मिलता है: x = 2π / 3। यूनिट सर्कल एक और जवाब देता है: -2π / 3।
   • x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π।
   • उदाहरण 3.tg (x - / 4) = 0.
   • उत्तर: x = / 4 + n।
   • उदाहरण 4. सीटीजी 2x = 1.732।
   • उत्तर: x = / 12 + n।
3. 3 त्रिकोणमितीय समीकरणों को हल करने के लिए प्रयुक्त रूपांतरण।
   • त्रिकोणमितीय समीकरणों को बदलने के लिए, बीजीय परिवर्तन (गुणन, सजातीय शब्दों की कमी, आदि) और त्रिकोणमितीय पहचान का उपयोग किया जाता है।
   • उदाहरण 5. त्रिकोणमितीय सर्वसमिकाओं का उपयोग करते हुए, समीकरण sin x + sin 2x + sin 3x = 0 को समीकरण 4cos x * sin (3x / 2) * cos (x / 2) = 0 में बदल दिया जाता है। इस प्रकार, आपको यह करने की आवश्यकता है निम्नलिखित मूल त्रिकोणमितीय समीकरणों को हल करें: cos x = 0; पाप (3x / 2) = 0; कॉस (x/2) = 0.
     
     
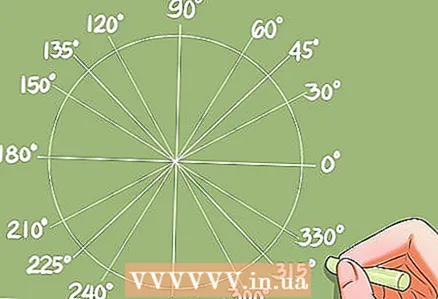
4. 4 कार्यों के ज्ञात मूल्यों से कोण ढूँढना।
   • त्रिकोणमितीय समीकरणों को हल करने के तरीकों को सीखने से पहले, आपको यह सीखना होगा कि कार्यों के ज्ञात मूल्यों से कोण कैसे खोजें। यह एक रूपांतरण तालिका या कैलकुलेटर का उपयोग करके किया जा सकता है।
   • उदाहरण: कॉस x = 0.732। कैलकुलेटर उत्तर x = 42.95 डिग्री देगा। यूनिट सर्कल अतिरिक्त कोण देगा, जिसकी कोज्या भी 0.732 है।
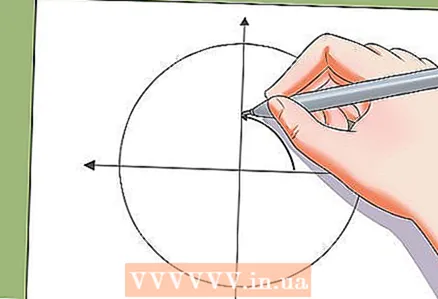5. 5 समाधान को यूनिट सर्कल पर एक तरफ सेट करें।
   • आप इकाई वृत्त पर त्रिकोणमितीय समीकरण के समाधान को स्थगित कर सकते हैं। इकाई वृत्त पर त्रिकोणमितीय समीकरण के समाधान एक नियमित बहुभुज के शीर्ष होते हैं।
   • उदाहरण: इकाई वृत्त पर हल x = π / 3 + πn / 2 एक वर्ग के शीर्ष हैं।
   • उदाहरण: यूनिट सर्कल पर समाधान x = π / 4 + πn / 3 एक नियमित षट्भुज के शीर्षों का प्रतिनिधित्व करते हैं।
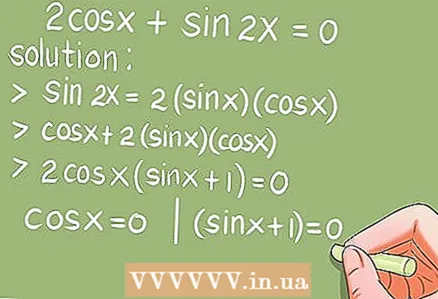6. 6 त्रिकोणमितीय समीकरणों को हल करने के तरीके।
   • यदि किसी दिए गए त्रिकोणमितीय समीकरण में केवल एक त्रिकोणमिति फलन है, तो उस समीकरण को मूल त्रिकोणमितीय समीकरण के रूप में हल करें।यदि किसी दिए गए समीकरण में दो या दो से अधिक त्रिकोणमितीय फलन शामिल हैं, तो ऐसे समीकरण को हल करने की 2 विधियाँ हैं (इसके परिवर्तन की संभावना के आधार पर)।
     • विधि १।
   • इस समीकरण को फॉर्म के समीकरण में बदलें: f (x) * g (x) * h (x) = 0, जहां f (x), g (x), h (x) मूल त्रिकोणमितीय समीकरण हैं।
     
     
   • उदाहरण 6.2cos x + sin 2x = 0. (0 x 2π)
   • समाधान। द्विकोण सूत्र का उपयोग करके sin 2x = 2 * sin x * cos x, sin 2x को प्रतिस्थापित करें।
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. अब दो मूल त्रिकोणमितीय समीकरणों को हल करें: cos x = 0 और (sin x + 1) = 0.
   • उदाहरण 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • हल: त्रिकोणमितीय सर्वसमिकाओं का उपयोग करते हुए, इस समीकरण को एक समीकरण में रूपांतरित करें: cos 2x (2cos x + 1) = 0. अब दो मूल त्रिकोणमितीय समीकरणों को हल करें: cos 2x = 0 और (2cos x + 1) = 0.
   • उदाहरण 8.sin x - sin 3x = cos 2x। (0 x 2π)
   • हल: त्रिकोणमितीय सर्वसमिकाओं का उपयोग करते हुए, इस समीकरण को इस रूप के समीकरण में रूपांतरित करें: -cos 2x * (2sin x + 1) = 0. अब दो मूल त्रिकोणमितीय समीकरणों को हल करें: cos 2x = 0 और (2sin x + 1) = 0.
     • विधि २।
   • दिए गए त्रिकोणमितीय समीकरण को केवल एक त्रिकोणमितीय फलन वाले समीकरण में बदलें। फिर इस त्रिकोणमितीय फलन को किसी अज्ञात से बदलें, उदाहरण के लिए, t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t, आदि)।
   • उदाहरण 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π)।
   • समाधान। इस समीकरण में, (cos ^ 2 x) को (1 - sin ^ 2 x) (पहचान द्वारा) से बदलें। रूपांतरित समीकरण है:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. sin x को t से बदलें। समीकरण अब इस तरह दिखता है: 5t ^ 2 - 4t - 9 = 0. यह दो जड़ों वाला एक द्विघात समीकरण है: t1 = -1 और t2 = 9/5। दूसरा रूट t2 फ़ंक्शन के मानों की श्रेणी (-1 sin x 1) को संतुष्ट नहीं करता है। अब तय करें: t = sin x = -1; एक्स = 3π / 2।
   • उदाहरण 10.tg x + 2 tg ^ 2 x = ctg x + 2
   • समाधान। tg x को t से बदलें। मूल समीकरण को इस प्रकार फिर से लिखें: (2t + 1) (t ^ 2 - 1) = 0. अब t ज्ञात करें और फिर t = tg x के लिए x ज्ञात करें।
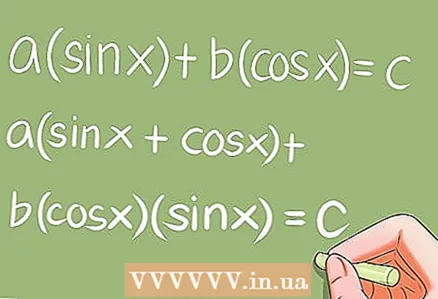7. 7 विशेष त्रिकोणमितीय समीकरण।
   • कई विशेष त्रिकोणमितीय समीकरण हैं जिन्हें विशिष्ट परिवर्तनों की आवश्यकता होती है। उदाहरण:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
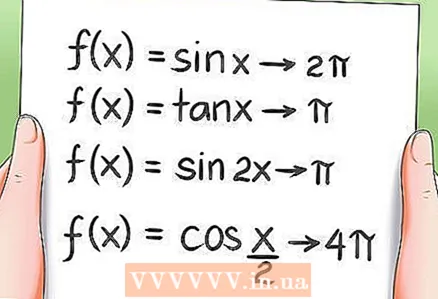8. 8 त्रिकोणमितीय कार्यों की आवधिकता।
   • जैसा कि पहले उल्लेख किया गया है, सभी त्रिकोणमितीय कार्य आवधिक होते हैं, अर्थात उनके मान एक निश्चित अवधि के बाद दोहराए जाते हैं। उदाहरण:
     • फलन f (x) = sin x का आवर्त 2π है।
     • फलन f (x) = tan x का आवर्त π के बराबर है।
     • फलन f (x) = sin 2x का आवर्त है।
     • फलन f (x) = cos (x / 2) की अवधि 4π है।
   • यदि समस्या में अवधि निर्दिष्ट है, तो इस अवधि के भीतर "x" मान की गणना करें।
   • नोट: त्रिकोणमितीय समीकरणों को हल करना आसान काम नहीं है और अक्सर त्रुटियाँ हो जाती हैं। इसलिए अपने उत्तरों को ध्यान से देखें। ऐसा करने के लिए, आप दिए गए समीकरण R (x) = 0 को प्लॉट करने के लिए एक रेखांकन कैलकुलेटर का उपयोग कर सकते हैं। ऐसे मामलों में, समाधान दशमलव अंशों के रूप में प्रस्तुत किए जाएंगे (अर्थात π को 3.14 से बदल दिया जाता है)।