विषय

• कदम बढ़ाने के लिए
• विधि 1 की 2: विकर्णों को ड्रा करें
• विधि 2 की 2: विकर्ण के लिए सूत्र का उपयोग करना

बहुभुज में विकर्णों को खोजना गणित में आगे बढ़ने के लिए एक आवश्यक कौशल है। यह पहली बार में मुश्किल लग सकता है, लेकिन मूल सूत्र सीखने के बाद यह काफी आसान है। एक विकर्ण एक बहुभुज के कोने के बीच खींचा गया कोई खंड है जिसमें उस बहुभुज के किनारे नहीं होते हैं। एक बहुभुज किसी भी आकार है जिसमें तीन से अधिक पक्ष हैं। एक बहुत ही सरल सूत्र का उपयोग करके, आप प्रत्येक बहुभुज में विकर्णों की संख्या की गणना कर सकते हैं, चाहे उसके चार पक्ष हों या 4000 पक्ष।

कदम बढ़ाने के लिए

विधि 1 की 2: विकर्णों को ड्रा करें

1. विभिन्न बहुभुजों के नाम जानते हैं। आपको पहले यह निर्धारित करने की आवश्यकता हो सकती है कि बहुभुज के कितने किनारे हैं। प्रत्येक बहुभुज में एक उपसर्ग होता है जो पक्षों की संख्या को इंगित करता है। यहाँ बहुभुज के नाम बीस भुजाओं के हैं:
   • चार-तरफा / टेट्रागोनिक: 4 पक्ष
   • पेंटागन / पेंटागन: 5 पक्ष
   • षट्कोण / षट्भुज: 6 भुजाएँ
   • हेप्टागन: 7 पक्ष
   • अष्टकोण / अष्टकोण: 8 भुजाएँ
   • नॉनगन / एननेगॉन: 9 पक्ष
   • दशांश: 10 भुजाएँ
   • हेंडकेगन: 11 पक्ष
   • डोडेकागन: 12 पक्ष
   • ट्रिसकाइडेकागून: 13 पक्ष
   • टेट्राडेकोगन: 14 पक्ष
   • पेंटाडेकॉन: 15 पक्ष
   • हेक्साडेकोगन: 16 पक्ष
   • हेप्टाडेकॉन: 17 पक्ष
   • अष्टकवर्ग: १। पक्ष
   • एननीया डिकैगन: 19 पक्ष
   • इकोसागून: 20 पक्ष
   • ध्यान दें कि एक त्रिकोण में कोई विकर्ण नहीं है।
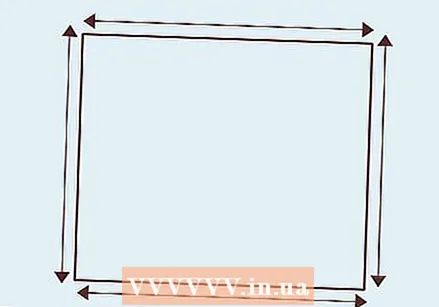2. बहुभुज ड्रा करें। यदि आप जानना चाहते हैं कि एक वर्ग में कितने विकर्ण हैं, तो वर्ग को आरेखित करके शुरू करें। विकर्णों को खोजने और गिनने का सबसे आसान तरीका बहुभुज को सममित रूप से खींचना है, प्रत्येक पक्ष की लंबाई समान है। यह ध्यान रखना महत्वपूर्ण है कि भले ही बहुभुज सममित न हो, फिर भी इसमें समान संख्या में विकर्ण होते हैं।
   • बहुभुज को खींचने के लिए, एक शासक का उपयोग करें और सभी पक्षों को जोड़ते हुए प्रत्येक पक्ष को समान लंबाई खींचें।
   • यदि आप सुनिश्चित नहीं हैं कि बहुभुज कैसा दिखता है, तो ऑनलाइन छवियों की खोज करें। उदाहरण के लिए, एक स्टॉप साइन एक अष्टकोना है।
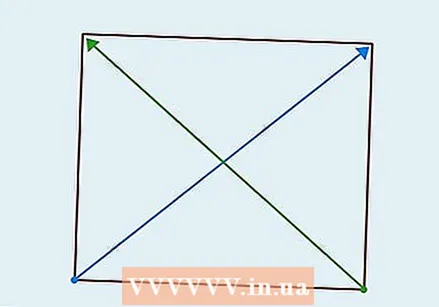3. विकर्णों को आकर्षित करें। एक विकर्ण एक ऐसा खंड है जो आकृति के एक कोने से दूसरे तक, बहुभुज के किनारों को छोड़कर खींचा जाता है। एक शासक का उपयोग किसी भी अन्य उपलब्ध शीर्ष पर विकर्ण को आकर्षित करने के लिए करें।
   • एक वर्ग के लिए, नीचे बाएँ कोने से ऊपरी दाएं कोने तक एक रेखा खींचें और नीचे दाएं कोने से ऊपरी बाएँ कोने तक एक और रेखा।
   • आसान गिनती के लिए विभिन्न रंगों में विकर्णों को आकर्षित करें।
   • ध्यान दें कि यह विधि बहुभुज के साथ दस से अधिक पक्षों के साथ बहुत अधिक कठिन हो जाती है।
4. विकर्णों की गणना करें। विकर्णों की गिनती के लिए दो विकल्प हैं: जब आप विकर्णों को खींचते हैं या जब वे खींचते हैं तो आप उन्हें गिन सकते हैं। प्रत्येक विकर्ण की गिनती करते समय, यह इंगित करने के लिए विकर्ण के ऊपर एक छोटी संख्या लिखें कि इसे गिना गया है। कई विकर्ण मिश्रित होने पर गिनती करते समय ट्रैक खोना आसान है।
   • वर्ग के लिए, दो विकर्ण हैं: प्रत्येक दो कोने के लिए एक विकर्ण।
   • एक षट्भुज में नौ विकर्ण होते हैं: प्रत्येक तीन कोने के लिए तीन विकर्ण होते हैं।
   • एक हेप्टागन में 14 विकर्ण हैं। हेप्टागोन से परे, विकर्णों को गिनना अधिक कठिन हो जाता है क्योंकि बहुत सारे विकर्ण होते हैं।
5. सावधान रहें कि विकर्णों को एक से अधिक बार न गिनें। प्रत्येक शीर्ष पर कई विकर्ण हो सकते हैं, लेकिन इसका मतलब यह नहीं है कि विकर्णों की संख्या विकर्णों की संख्या के बराबर होती है जबकि विकर्णों की संख्या। विकर्णों की गिनती करते समय, सुनिश्चित करें कि आप केवल प्रत्येक विकर्ण को एक बार गिनते हैं।
   • उदाहरण के लिए, एक पंचकोण (पाँच भुजाएँ) में केवल पाँच विकर्ण होते हैं। प्रत्येक शीर्ष पर दो विकर्ण होते हैं, इसलिए यदि आपने प्रत्येक शीर्ष के प्रत्येक विकर्ण को दो बार गिना है, तो आपको लगेगा कि 10 विकर्ण हैं। यह गलत है क्योंकि आपने प्रत्येक विकर्ण को दो बार गिना है!
6. कुछ उदाहरणों के साथ अभ्यास करें। कुछ अन्य बहुभुज बनाएं और विकर्णों की संख्या गिनें। बहुभुज को इस विधि के काम करने के लिए सममित नहीं होना पड़ता है।एक खोखले बहुभुज के मामले में, आपको वास्तविक बहुभुज के बाहर कुछ विकर्ण खींचने की आवश्यकता हो सकती है।
   • एक षट्भुज या षट्भुज में 9 विकर्ण होते हैं।
   • एक हेप्टागन में 14 विकर्ण हैं।

विधि 2 की 2: विकर्ण के लिए सूत्र का उपयोग करना

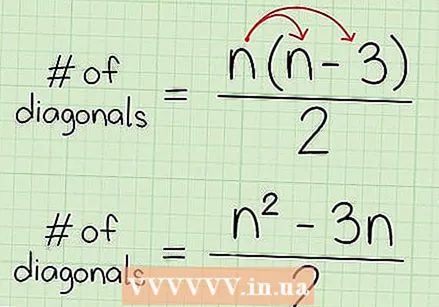1. सूत्र को परिभाषित करें। बहुभुज के विकर्णों की संख्या ज्ञात करने का सूत्र n (n-3) / 2 है जहाँ "n" बहुभुज के पक्षों की संख्या के बराबर है। वितरण संपत्ति का उपयोग करते हुए, इसे (n - 3n) / 2 के रूप में फिर से लिखा जा सकता है। आप इसे दोनों दिशाओं में देख सकते हैं, दोनों समीकरण समान हैं।
   • इस समीकरण का उपयोग किसी भी बहुभुज के विकर्णों की संख्या ज्ञात करने के लिए किया जा सकता है।
   • ध्यान दें कि त्रिकोण इस नियम का एक अपवाद है। त्रिकोण के आकार के कारण, इसमें कोई विकर्ण नहीं है।
2. बहुभुज के पक्षों की संख्या निर्धारित करें। इस सूत्र का उपयोग करने के लिए, आपको बहुभुज के पक्षों की संख्या जानने की आवश्यकता है। बहुभुज के नाम पर पक्षों की संख्या दी गई है, इसलिए आपको बस यह जानना होगा कि प्रत्येक नाम का क्या अर्थ है। यहाँ कुछ सामान्य उपसर्ग हैं जिनका आप बहुभुज से सामना कर सकते हैं:
   • टेट्रा (4), पेंटा (5), हेक्सा (6), हेप्टा (7), ऑक्टा (8), एननीया (9), डेका (10), हेंडेका (11), डोडेका (12), त्रिदेका (13), tetradeca (14), pentadeca (15), आदि।
   • कई पक्षों के साथ बहुत बड़े बहुभुज के लिए, आप बस "एन-गून" देख सकते हैं, जहां "एन" पक्षों की संख्या है। उदाहरण के लिए, एक 44-पक्षीय बहुभुज को 44-गुंडे के रूप में लिखा जाता है।
   • यदि आपको बहुभुज की तस्वीर मिलती है, तो आप बस पक्षों की संख्या गिन सकते हैं।
3. समीकरण में पक्षों की संख्या शामिल करें। एक बार जब आपको पता चलता है कि बहुभुज के कितने पक्ष हैं, तो आपको बस उस संख्या को समीकरण में रखना है और समीकरण को हल करना है। जहां भी आप समीकरण में "एन" देखते हैं, बहुभुज के पक्षों की संख्या को बहुभुज के पक्षों की संख्या से बदल दिया जाता है।
   • उदाहरण के लिए: एक डोडेकागन के 12 पक्ष हैं।
   • समीकरण लिखें: n (n-3) / 2
   • इसे चर में संसाधित करें: (12 (12 - 3)) / 2
4. प्रश्न हल करें। अंत में, संचालन के सही क्रम में समीकरण को हल करें। घटाव, फिर गुणा, और अंत में विभाजन को हल करके शुरू करें। अंतिम उत्तर बहुभुज के विकर्णों की संख्या है।
   • उदाहरण के लिए: (12 (12 - 3)) / 2
   • घटाना: (12 * 9) / 2
   • गुणा: (१०ip) / २
   • शेयर: 54
   • तो एक डोडेकोगन में 54 विकर्ण हैं।
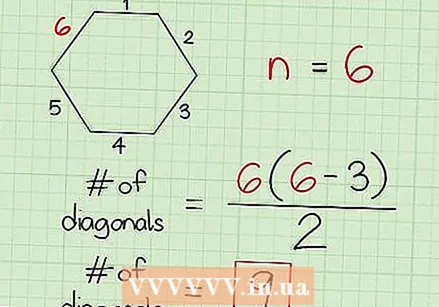5. अधिक उदाहरणों के साथ अभ्यास करें। गणित की अवधारणा के साथ आपके पास जितना अधिक अभ्यास होगा, आप इसका बेहतर उपयोग कर सकते हैं। कई अभ्यास अभ्यासों को पूरा करने से आपको क्विज़, टेस्ट या परीक्षा के लिए ज़रूरी फॉर्मूला याद रखने में भी मदद मिलेगी। याद रखें, यह सूत्र बहुभुज के लिए काम करता है जिसमें तीन से अधिक पक्ष होते हैं।
   • षट्कोण (6 भुजाएँ): n (n-3) / 2 = 6 (6-3) / 2 = 6 * 3/2 = 18/2 = 9 विकर्ण।
   • दशांश (10 भुजाएँ): n (n-3) / 2 = 10 (10-3) / 2 = 10 * 7/2 = 70/2 = 35 विकर्ण।
   • इकोसैगन (20 पक्ष): n (n-3) / 2 = 20 (20-3) / 2 = 20 * 17/2 = 340/2 = 170 विकर्ण।
   • 96-गून (96 पक्ष): 96 (96-3) / 2 = 96 * 93/2 = 8928/2 = 4464 विकर्ण।