विषय

• कदम
• सलाह

यदि आप एक गणितज्ञ या ग्राफिक प्रोग्रामर हैं, तो आपको संभवतः दो दिए गए वैक्टरों के बीच का कोण खोजना होगा। इस लेख में, wikiHow आपको दिखाता है कि कैसे करना है।

कदम

भाग 1 का 2: दो वैक्टर के बीच का कोण ज्ञात कीजिए

1. 

   वेक्टर परिभाषा आपके पास जो दो वैक्टर हैं, उनके बारे में सभी जानकारी नीचे लिखें। मान लें कि आपके पास केवल उनके आयामी निर्देशांक (जिन्हें घटक भी कहा जाता है) के निर्दिष्ट पैरामीटर हैं। यदि आप पहले से ही एक वेक्टर की लंबाई (परिमाण) जानते हैं, तो आप नीचे दिए गए कुछ चरणों को छोड़ सकते हैं।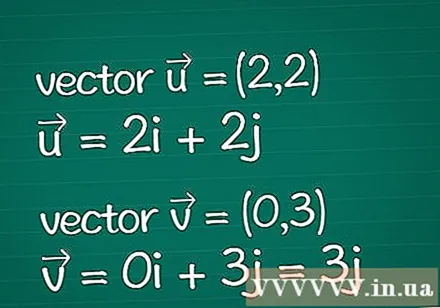
   • उदाहरण: दो आयामी वेक्टर = (2,2) और दो आयामी वेक्टर = (0,3)। उन्हें = 2 के रूप में भी लिखा जा सकता हैमैं + 2जे और = 0मैं + 3जे = 3जे.
   • यद्यपि इस लेख में दो-आयामी वैक्टर उदाहरण में उपयोग किए गए हैं, निम्न निर्देश किसी भी संख्या में आयामों के साथ वैक्टर पर लागू हो सकते हैं।

2. 

   
   
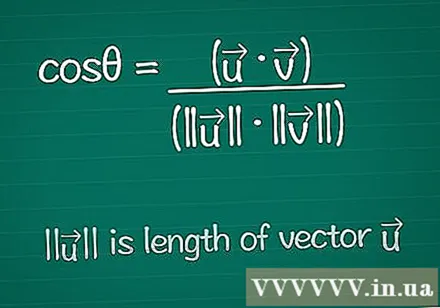
   कोसाइन सूत्र लिखिए। दो वैक्टर के बीच के कोण को खोजने के लिए, हम उस कोण के लिए कोसाइन को खोजने के सूत्र के साथ शुरू करते हैं। आप इस सूत्र के बारे में नीचे जान सकते हैं, या इसे इस तरह लिख सकते हैं:
   • cos = (•) / (|||| ||||)
   • |||| का अर्थ है "वेक्टर की लंबाई"।
   • • दो वैक्टर का अदिश उत्पाद है - इसे नीचे समझाया जाएगा।

3. 

   
   
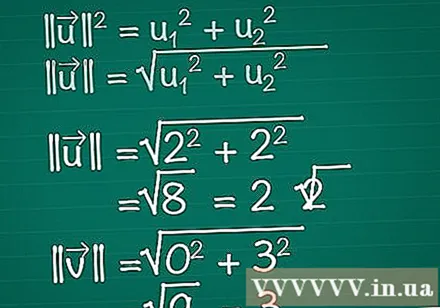
   प्रत्येक वेक्टर की लंबाई की गणना करें। कल्पना कीजिए कि एक सही त्रिभुज वेक्टर के x, y घटकों और स्वयं वेक्टर से बना है। वेक्टर त्रिभुज का कर्ण बनाता है, इसलिए इसकी लंबाई जानने के लिए हम पाइथागोरस प्रमेय का उपयोग करते हैं। वास्तव में, इस सूत्र को आसानी से किसी भी आयाम के आयामों तक बढ़ाया जा सकता है।
   • || यू || = यू₁ + यू₂। यदि एक वेक्टर में दो से अधिक तत्व हैं, तो आपको बस + u जोड़ते रहना होगा₃ + यू₄ +...
   • इसलिए, द्वि-आयामी वेक्टर के लिए, || यू || = = (यू₁ + यू₂).
   • इस उदाहरण में, ||| = = (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
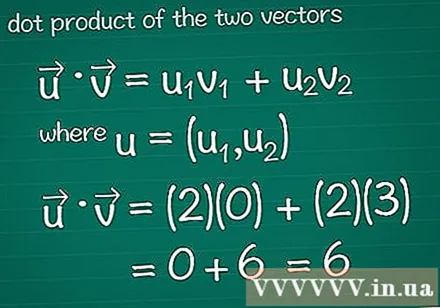
   दो वैक्टर के अदिश उत्पाद की गणना करें। शायद आपने वेक्टर गुणन की विधि सीखी है, जिसे रूप में भी जाना जाता है अदिश यह। उनकी संरचना के सापेक्ष स्केलर उत्पाद की गणना करने के लिए, प्रत्येक दिशा में अवयवों को एक साथ गुणा करें, फिर संपूर्ण परिणाम जोड़ें।
   • ग्राफिक्स प्रोग्राम के लिए, कृपया आगे पढ़ने से पहले युक्तियों को देखें।
   • गणित में • = यू₁v₁ + यू₂v₂, कहां, यू = (यू₁, आप यू₂)। यदि वेक्टर में दो से अधिक तत्व हैं, तो बस + u जोड़ें₃v₃ + यू₄v₄...
   • इस उदाहरण में, • = यू₁v₁ + यू₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6। यह वेक्टर और वेक्टर का अदिश उत्पाद है।

5. 

   परिणाम सूत्र में रखें। याद रखें कि cos| = (•) / (|||| ||) || अब हम स्केलर उत्पाद और प्रत्येक वेक्टर की लंबाई दोनों जानते हैं। कोण के कोसाइन की गणना करने के सूत्र में इन्हें दर्ज करें।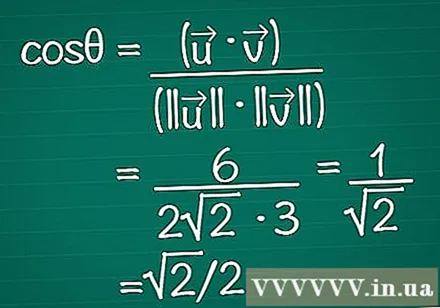
   • हमारे उदाहरण में, cos our = 6 / (2 example2 * 3) = 1 / =2 = θ2 / 2।

6. 

   इसके कोसाइन पर आधारित कोण का पता लगाएं। आप किसी ज्ञात कॉस् मान से θ को खोजने के लिए एक कैलकुलेटर में आर्कॉस या कॉस फ़ंक्शन का उपयोग कर सकते हैं। कुछ परिणामों के साथ, आपको यूनिट सर्कल के आधार पर कोण मिल सकता है।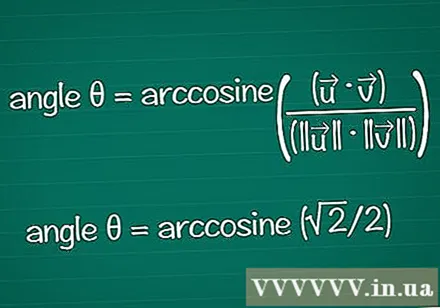
   • उदाहरण में, कोण को खोजने के लिए अपने कैलकुलेटर में cos the = √2 / 2. "arccos (/2 / 2)" दर्ज करें। या, आप इकाई the पर कोण θ पा सकते हैं, स्थिति cos√ = /2 / 2. पर θ = /₄ या 45 or.
   • सब कुछ मिलाकर, अंतिम सूत्र है: कोण everything = arccosine ((•) / ((||||)) ||
   विज्ञापन

भाग 2 का 2: कोण सूत्र का निर्धारण

1. 

   सूत्र के उद्देश्य को समझें। यह सूत्र मौजूदा नियमों से नहीं लिया गया था। इसके बजाय, यह स्केलर उत्पाद की परिभाषा और दो वैक्टर के बीच के कोण के रूप में बनता है। फिर भी, यह एक मनमाना निर्णय नहीं था। बुनियादी ज्यामिति पर वापस जाकर, हम समझ सकते हैं कि यह सूत्र सहज और उपयोगी परिभाषा क्यों प्रदान करता है।
   • नीचे दिए गए उदाहरण दो आयामी वैक्टर का उपयोग करते हैं क्योंकि वे समझना आसान और सरल हैं। तीन आयामी या अधिक वैक्टर में लगभग समान सामान्य सूत्रों द्वारा परिभाषित गुण होते हैं।

2. 

   कोसाइन की प्रमेय की समीक्षा करें। पक्षों और ए के बीच के कोण के विपरीत कोण, के साथ एक साधारण त्रिकोण पर विचार करें। कोसाइन प्रमेय में कहा गया है कि c = a + b -2abक्योंकि(Θ)। यह परिणाम बुनियादी ज्यामिति से काफी सरलता से लिया गया है।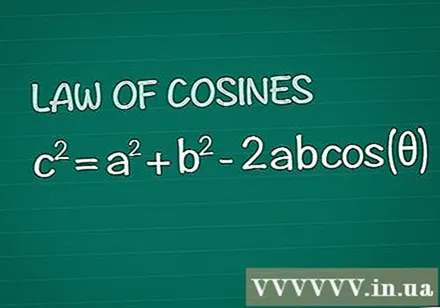

3. 

   एक त्रिकोण बनाते हुए, दो वैक्टर कनेक्ट करें। कागज, वैक्टर और वैक्टर पर दो-आयामी वैक्टर की एक जोड़ी बनाएं, जिनके बीच-कोण होता है। त्रिभुज बनाने के लिए इन दोनों के बीच एक तीसरा वेक्टर बनाएं। दूसरे शब्दों में, एक सदिश को खींचिए ऐसा + =। सदिश = -।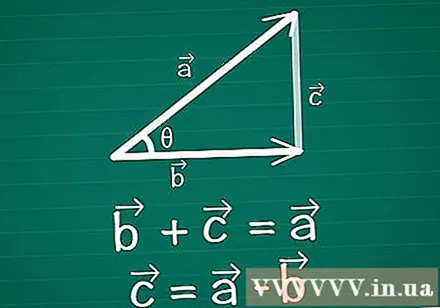

4. 

   इस त्रिभुज के लिए कोसाइन प्रमेय लिखिए। कोसाइन प्रमेय में हमारे "सदिश त्रिकोण" की साइड लंबाई को प्रतिस्थापित करें:
   • || (ए - बी) || = || ए || + || बी || - 2 || ए || || बी ||क्योंकि(θ)

5. 

   स्केलर उत्पाद के साथ फिर से लिखना। याद रखें, एक स्केलर उत्पाद दूसरे पर एक वेक्टर की छवि है। अपने आप से किसी वेक्टर के स्केलर उत्पाद को प्रक्षेपण की आवश्यकता नहीं है, क्योंकि यहां, दिशा में कोई अंतर नहीं है। इसका अर्थ है कि || = || a || इसका उपयोग करते हुए, हम समीकरण को फिर से लिखते हैं:
   • (-) • (-) = • + • - 2 || ए || || बी ||क्योंकि(θ)

6. 

   सफलतापूर्वक उसी सूत्र को फिर से लिखना। सूत्र के बाईं ओर का विस्तार करें, फिर कोण को खोजने के लिए उपयोग किए जाने वाले सूत्र को प्राप्त करने के लिए सरल करें।
   • • - • - • + • = • + • - 2 || एक || || बी ||क्योंकि(θ)
   • - • - • = -2 || ए || || बी ||क्योंकि(θ)
   • -2 (•) = -2 || एक || || बी ||क्योंकि(θ)
   • • = || a || || बी ||क्योंकि(θ)
   विज्ञापन

सलाह

• मूल्यों को बदलने और समस्या को जल्दी से हल करने के लिए, दो-आयामी वैक्टर की किसी भी जोड़ी के लिए इस सूत्र का उपयोग करें: cosθ = (u)₁ • वी₁ + यू₂ • वी₂) / (√ (यू)₁ • आप₂) • v (v)₁ • वी₂)).
• यदि आप कंप्यूटर ग्राफिक्स सॉफ़्टवेयर के साथ काम कर रहे हैं, तो संभावना है कि आपको केवल वेक्टर के आयामों के बारे में उनकी लंबाई के बारे में चिंता किए बिना चिंता करनी होगी। एक समीकरण को छोटा करने और अपने कार्यक्रम को गति देने के लिए निम्नलिखित चरणों का उपयोग करें:
  • प्रत्येक वेक्टर को सामान्य करें ताकि वे 1 के बराबर हों। ऐसा करने के लिए, वेक्टर के प्रत्येक घटक को उसकी लंबाई से विभाजित करें।
  • मूल वेक्टर के बजाय स्केलर का सामान्यीकृत उत्पाद प्राप्त करें।
  • चूंकि लंबाई 1 है, हम समीकरण से लंबाई के तत्वों को बाहर कर सकते हैं। अंत में, प्राप्त कोण समीकरण arccos (•) है।
• कोसाइन फॉर्मूले के आधार पर, हम जल्दी से यह निर्धारित कर सकते हैं कि कोण तीव्र है या आपत्तिजनक है। Cos| = (•) / ((|| ||||) से प्रारंभ करें:
  • समीकरण के बाईं और दाईं ओर समान चिह्न (सकारात्मक या नकारात्मक) होना चाहिए।
  • चूंकि लंबाई हमेशा सकारात्मक होती है, इसलिए cosθ में स्केलर उत्पाद के समान चिन्ह होना चाहिए।
  • इसलिए, यदि उत्पाद सकारात्मक है, तो cosθ भी सकारात्मक है। हम, <2/2 या 90 the के साथ, यूनिट सर्कल के पहले चतुर्थांश में हैं। खोजने के लिए कोण तेज कोण है।
  • यदि अदिश उत्पाद ऋणात्मक है, तो cosθ ऋणात्मक है। हम, / 2 <≤ the π या 90º <º θ 180θ के साथ इकाई चक्र के दूसरे चतुर्थांश में हैं। वह जेल का कोना है।